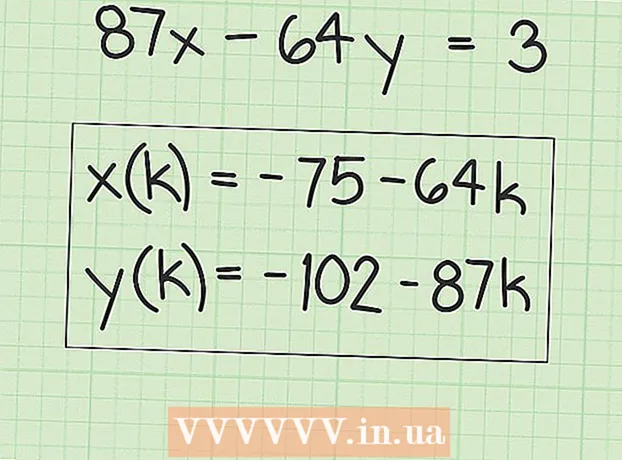
Sisu

• Sammud
• Osa 1: 4: Kuidas võrrandit kirjutada
• Osa 2/4: Kuidas kirjutada Eukleidese algoritmi
• Osa 3/4: Kuidas leida lahendus Eukleidese algoritmi abil?
• Osa 4/4: otsige lõpmatuid lahendusi

Lineaarse diofantilise võrrandi lahendamiseks peate leidma muutujate "x" ja "y" väärtused, mis on täisarvud. Täisarvuline lahendus on tavalisest keerulisem ja nõuab teatud toimingute komplekti. Esiteks peate arvutama koefitsientide suurima ühise jagaja (GCD) ja seejärel leidma lahenduse. Kui olete leidnud lineaarvõrrandile ühe täisarvulise lahenduse, saate lihtsa mustri abil leida lõpmatu hulga muid lahendusi.

Sammud

Osa 1: 4: Kuidas võrrandit kirjutada

1. 1 Kirjutage võrrand standardkujul alla. Lineaarvõrrand on võrrand, milles muutujate astendajad ei ületa 1. Sellise lineaarvõrrandi lahendamiseks kirjutage see esmalt standardkujul. Lineaarvõrrandi standardvorm näeb välja selline: ${ displaystyle Ax + By = C}$, kus ${ displaystyle A, B}$ ja ${ displaystyle C}$ - täisarvud.
   • Kui võrrand on antud erineval kujul, viige see standardvormi, kasutades algebralisi põhitehteid. Näiteks võrrandit arvestades ${ displaystyle 23x + 4y -7x = -3y + 15}$... Andke sarnased terminid ja kirjutage võrrand järgmiselt: ${ displaystyle 16x + 7y = 15}$.
2. 2 Lihtsustage võrrandit (kui võimalik). Kui kirjutate võrrandi standardkujul, vaadake koefitsiente ${ displaystyle A, B}$ ja ${ displaystyle C}$... Kui neil koefitsientidel on GCD, jagage kõik kolm koefitsienti sellega. Sellise lihtsustatud võrrandi lahendus on ka lahendus algsele võrrandile.
   • Näiteks kui kõik kolm koefitsienti on paaris, jagage need vähemalt kahega. Näiteks:
     • ${ displaystyle 42x + 36y = 48}$ (kõik liikmed jaguvad 2 -ga)
     • ${ displaystyle 21x + 18y = 24}$ (nüüd on kõik liikmed jagatud 3 -ga)
     • ${ displaystyle 7x + 6y = 8}$ (seda võrrandit ei saa enam lihtsustada)
3. 3 Kontrollige, kas võrrandit saab lahendada. Mõnel juhul võite kohe öelda, et võrrandil pole lahendusi. Kui koefitsient "C" ei jagu koefitsientide "A" ja "B" GCD -ga, pole võrrandil lahendusi.
   • Näiteks kui mõlemad koefitsiendid ${ displaystyle A}$ ja ${ displaystyle B}$ on ühtlased, siis koefitsient ${ displaystyle C}$ peab olema ühtlane. Aga kui ${ displaystyle C}$ kummaline, siis pole lahendust.
     • Võrrand ${ displaystyle 2x + 4y = 21}$ pole täisarvulisi lahendusi.
     • Võrrand ${ displaystyle 5x + 10y = 17}$ täisarvulisi lahendusi pole, kuna võrrandi vasak pool jagub 5 -ga ja parem pool mitte.

Osa 2/4: Kuidas kirjutada Eukleidese algoritmi

1. 1 Saage aru Eukleidese algoritmist. See on korduvate jagunemiste jada, kus järgmist jagurit kasutatakse eelmist jääki. Viimane jagaja, mis jagab arvud integraalselt, on kahe numbri suurim ühine jagaja (GCD).
   • Näiteks leidkem numbrite 272 ja 36 GCD, kasutades Eukleidese algoritmi:
     • ${ displaystyle 272 = 7 * 36 + 20}$ - jagage suurem arv (272) väiksemaga (36) ja pöörake tähelepanu ülejäänud osale (20);
     • ${ displaystyle 36 = 1 * 20 + 16}$ - jagage eelmine jagaja (36) eelmise jäägiga (20). Pange tähele uut jääki (16);
     • ${ displaystyle 20 = 1 * 16 + 4}$ - jagage eelmine jagaja (20) eelmise jäägiga (16). Märkige uus jääk (4);
     • ${ displaystyle 16 = 4 * 4 + 0}$ - Jagage eelmine jagaja (16) eelmise jäägiga (4). Kuna ülejäänud osa on 0, võime öelda, et 4 on kahe algse numbri 272 ja 36 GCD.
2. 2 Koefitsientidele "A" ja "B" rakendage Eukleidese algoritmi. Kui kirjutate lineaarvõrrandi standardkujul, määrake koefitsiendid "A" ja "B" ning seejärel rakendage neile GCD leidmiseks Eukleidese algoritm. Näiteks antud lineaarvõrrand ${ displaystyle 87x-64y = 3}$.
   • Siin on Eukleidese algoritm koefitsientide A = 87 ja B = 64 jaoks:
     • ${ displaystyle 87 = 1 * 64 + 23}$
     • ${ displaystyle 64 = 2 * 23 + 18}$
     • ${ displaystyle 23 = 1 * 18 + 5}$
     • ${ displaystyle 18 = 3 * 5 + 3}$
     • ${ displaystyle 5 = 1 * 3 + 2}$
     • ${ displaystyle 3 = 1 * 2 + 1}$
     • ${ displaystyle 2 = 2 * 1 + 0}$
3. 3 Leidke suurim ühine tegur (GCD). Kuna viimane jagaja oli 1, siis GCD 87 ja 64 on 1. Seega on 87 ja 64 teineteise suhtes algarvud.
4. 4 Analüüsige tulemust. Kui leiate gcd koefitsiendid ${ displaystyle A}$ ja ${ displaystyle B}$, võrrelge seda koefitsiendiga ${ displaystyle C}$ algne võrrand. Kui ${ displaystyle C}$ jagatav gcd -ga ${ displaystyle A}$ ja ${ displaystyle B}$, võrrandil on täisarvuline lahendus; vastasel juhul pole võrrandil lahendusi.
   • Näiteks võrrand ${ displaystyle 87x-64y = 3}$ saab lahendada, sest 3 jagub 1 -ga (gcd = 1).
   • Oletame näiteks, et GCD = 5. 3 ei ole ühtlaselt jagatav 5 -ga, seega pole sellel võrrandil täisarvulisi lahendeid.
   • Nagu allpool näidatud, kui võrrandil on üks täisarvuline lahendus, on sellel ka lõpmatu arv muid täisarvulisi lahendeid.

Osa 3/4: Kuidas leida lahendus Eukleidese algoritmi abil?

1. 1 Numeerige GCD arvutamise sammud. Lineaarvõrrandi lahenduse leidmiseks peate asendus- ja lihtsustamisprotsessi aluseks võtma Eukleidese algoritmi.
   • Alustage GCD arvutamise sammude nummerdamisega. Arvutusprotsess näeb välja selline:
     • ${ displaystyle { text {Step 1}}: 87 = (1 * 64) +23}$
     • ${ displaystyle { text {Step 2}}: 64 = (2 * 23) +18}$
     • ${ displaystyle { text {3. samm}}: 23 = (1 * 18) +5}$
     • ${ displaystyle { text {Step 4}}: 18 = (3 * 5) +3}$
     • ${ displaystyle { text {Step 5}}: 5 = (1 * 3) +2}$
     • ${ displaystyle { text {6. samm}}: 3 = (1 * 2) +1}$
     • ${ displaystyle { text {Step 7}}: 2 = (2 * 1) +0}$
2. 2 Pöörake tähelepanu viimasele sammule, kus on jääke. Ülejäänud eraldamiseks kirjutage selle sammu võrrand ümber.
   • Meie näites on viimane samm jäägiga samm 6. Järelejäänud on 1. Kirjutage 6. sammu võrrand ümber järgmiselt:
     • ${ displaystyle 1 = 3- (1 * 2)}$
3. 3 Isoleerige ülejäänud samm. See protsess on samm-sammult "ülespoole liikumine". Iga kord, kui eraldate ülejäänud sammu eelmise sammu võrrandist.
   • Eraldage ülejäänud võrrand sammus 5:
     • ${ displaystyle 2 = 5- (1 * 3)}$ või ${ displaystyle 2 = 5-3}$
4. 4 Asenda ja lihtsusta. Pange tähele, et sammu 6 võrrand sisaldab numbrit 2 ja sammu 5 võrrandis on number 2 isoleeritud. Seega asendage 6. sammu võrrandi „2” asemel 5. sammu avaldis:
   • ${ displaystyle 1 = 3-2}$ (sammu 6 võrrand)
   • ${ displaystyle 1 = 3- (5-3)}$ (2 asemel asendati väljend)
   • ${ displaystyle 1 = 3-5 + 3}$ (avatud sulgud)
   • ${ displaystyle 1 = 2 (3) -5}$ (lihtsustatud)
5. 5 Korrake asendamise ja lihtsustamise protsessi. Korrake kirjeldatud protsessi, liikudes vastupidises järjekorras läbi Eukleidese algoritmi. Iga kord, kui kirjutate eelmise sammu võrrandi ümber ja ühendate selle viimase saadud võrrandiga.
   • Viimane samm, mida me vaatasime, oli samm 5. Nii et minge 4. sammu juurde ja eraldage ülejäänud selle sammu võrrandist:
     • ${ displaystyle 3 = 18- (3 * 5)}$
   • Asendage see väljend viimases võrrandis "3":
     • ${ displaystyle 1 = 2 (18-3 * 5) -5}$
     • ${ displaystyle 1 = 2 (18) -6 (5) -5}$
     • ${ displaystyle 1 = 2 (18) -7 (5)}$
6. 6 Jätkake asendus- ja lihtsustamisprotsessiga. Seda protsessi korratakse, kuni jõuate Eukleidese algoritmi algsesse etappi. Protsessi eesmärk on kirjutada võrrand koos lahendatava algvõrrandi koefitsientidega 87 ja 64. Meie näites:
   • ${ displaystyle 1 = 2 (18) -7 (5)}$
   • ${ displaystyle 1 = 2 (18) -7 (23-18)}$ (asendas 3. sammu avaldise)
     • ${ displaystyle 1 = 2 (18) -7 (23) +7 (18)}$
     • ${ displaystyle 1 = 9 (18) -7 (23)}$
   • ${ displaystyle 1 = 9 (64-2 * 23) -7 (23)}$ (asendas 2. sammu avaldise)
     • ${ displaystyle 1 = 9 (64) -18 (23) -7 (23)}$
     • ${ displaystyle 1 = 9 (64) -25 (23)}$
   • ${ displaystyle 1 = 9 (64) -25 (87-64)}$ (asendas 1. sammu avaldise)
     • ${ displaystyle 1 = 9 (64) -25 (87) +25 (64)}$
     • ${ displaystyle 1 = 34 (64) -25 (87)}$
7. 7 Kirjutage saadud võrrand ümber vastavalt algsetele koefitsientidele. Kui naasete Eukleidese algoritmi esimese sammu juurde, näete, et saadud võrrand sisaldab kahte algvõrrandi koefitsienti. Kirjutage võrrand ümber nii, et selle terminite järjekord vastaks algse võrrandi koefitsientidele.
   • Meie näites on algne võrrand ${ displaystyle 87x-64y = 3}$... Seetõttu kirjutage saadud võrrand ümber nii, et koefitsiendid oleksid joondatud.Pöörake erilist tähelepanu koefitsiendile "64". Algses võrrandis on see koefitsient negatiivne ja Eukleidese algoritmis positiivne. Seetõttu tuleb tegur 34 muuta negatiivseks. Lõplik võrrand kirjutatakse järgmiselt:
     • ${ displaystyle 87 (-25) -64 (-34) = 1}$
8. 8 Lahenduse leidmiseks rakendage sobiv kordaja. Pange tähele, et meie näites on GCD = 1, seega on lõplik võrrand 1. Kuid algne võrrand (87x-64y) on 3. Seetõttu tuleb lahenduse saamiseks korrutada kõik lõpliku võrrandi terminid 3-ga:
   • ${ displaystyle 87 (-25 * 3) -64 (-34 * 3) = 1 * 3}$
   • ${ displaystyle 87 (-75) -64 (-102) = 3}$
9. 9 Kirjutage võrrandisse täisarvuline lahendus. Arvud, mis korrutatakse algse võrrandi koefitsientidega, on selle võrrandi lahendused.
   • Meie näites kirjutage lahendus koordinaatide paarina: ${ displaystyle (x, y) = ( - 75, -102)}$.

Osa 4/4: otsige lõpmatuid lahendusi

1. 1 Mõista, et lahendusi on lõpmata palju. Kui lineaarvõrrandil on üks täisarvuline lahendus, siis peab sellel olema lõpmatult palju täisarvulisi lahendeid. Siin on kiire tõestus (algebralisel kujul):
   • ${ displaystyle Ax + By = C}$
   • ${ displaystyle A (x + B) + B (y-A) = C}$ (kui lisate x -ile "B" ja lahutate "y" -st "A", siis algse võrrandi väärtus ei muutu)
2. 2 Salvestage algsed x ja y väärtused. Järgmiste (lõpmatute) lahenduste arvutamise mall algab ainsa juba leitud lahendusega.
   • Meie näites on lahendus koordinaatide paar ${ displaystyle (x, y) = ( - 75, -102)}$.
3. 3 Lisage "x" väärtusele tegur "B". Tehke seda uue x väärtuse leidmiseks.
   • Meie näites x = -75 ja B = -64:
     • ${ displaystyle x = -75 + ( - 64) = - 139}$
   • Seega uus väärtus "x": x = -139.
4. 4 Lahutage "y" väärtusest tegur "A". Et algse võrrandi väärtus ei muutuks, peate ühe numbri "x" lisamisel lahutama "y" -st teise numbri.
   • Meie näites y = -102 ja A = 87:
     • ${ displaystyle y = -102-87 = -189}$
   • Seega "y" uus väärtus: y = -189.
   • Uus koordinaatide paar kirjutatakse järgmiselt: ${ displaystyle (x, y) = ( - 139, -189)}$.
5. 5 Kontrollige lahendust. Veendumaks, et uus koordinaatpaar on lahendus algsele võrrandile, ühendage väärtused võrrandiga.
   • ${ displaystyle 87x-64y = 3}$
   • ${ displaystyle 87 (-139) -64 (-189) = 3}$
   • ${ displaystyle 3 = 3}$
   • Kuna võrdsus on saavutatud, on otsus õige.
6. 6 Kirjutage väljendeid, et leida palju lahendusi. "X" väärtused võrduvad algse lahendusega pluss mis tahes "B" teguri kordajaga. Seda saab kirjutada järgmise väljendina:
   • x (k) = x + k (B), kus “x (k)” on “x” väärtuste kogum ja “x” on teie leitud “x” algne (esimene) väärtus.
     • Meie näites:
     • ${ displaystyle x (k) = - 75-64k}$
   • y (k) = y-k (A), kus y (k) on y väärtuste kogum ja y on leitud algne (esimene) y väärtus.
     • Meie näites:
     • ${ displaystyle y (k) = - 102-87k}$