Sisu

• Sammud
• Osa 1 /3: Lihtsuse testid
• Osa 2/3: Kuidas lihtsustestid toimivad
• Osa 3 /3: Hiina järelejäänud teoreemi kasutamine
• Näpunäiteid
• Mida sul vaja on

Algarvud on arvud, mis jaguvad ainult iseenesest ja 1. Kõiki teisi numbreid nimetatakse liitarvudeks. Arvude esmaseks määramiseks on palju viise ja neil kõigil on oma eelised ja puudused. Ühest küljest on mõned meetodid väga täpsed, kuid kui tegemist on suurte arvudega, on need üsna keerulised. Teisest küljest on palju kiiremaid viise, kuid need võivad põhjustada valesid tulemusi. Sobiva meetodi valik sõltub sellest, kui suurte numbritega te töötate.

Sammud

Osa 1 /3: Lihtsuse testid

Märge: kõigis valemites n tähistab kontrollitavat numbrit.

1. 1 Jagajate loend. Piisab jagada n kõigile algarvudele 2 kuni ümardatud väärtuseni (${ displaystyle { sqrt {n}}}$).
2. 2 Fermati väike teoreem. Hoiatus: mõnikord tuvastab test komposiitnumbrid valesti, isegi kõigi a väärtuste puhul.
   • Valime täisarvu anii, et 2 ≤ a ≤ n - 1.
   • Kui a (mod n) = a (mod n), siis on arv arvatavasti algarv. Kui võrdsus pole täidetud, on arv n liitühend.
   • Kontrollige antud väärtust mitme väärtuse jaoks asuurendada tõenäosust, et testitav arv on tõepoolest peamine.
3. 3 Miller-Rabini test. Hoiatus: mõnikord, kuigi harva, mitme a väärtuse puhul tuvastab test liitarvud valesti algarvudena.
   • Leidke kogused s ja d nii, et ${ displaystyle n-1 = 2 ^ {s} * d}$.
   • Valige täisarv a vahemikus 2 ≤ a ≤ n - 1.
   • Kui a = +1 (mod n) või -1 (mod n), siis n on tõenäoliselt prime. Sellisel juhul minge testi tulemuse juurde. Kui võrdsus ei kehti, jätkake järgmise sammuga.
   • Pane oma vastus ruudu alla (${ displaystyle a ^ {2d}}$). Kui saate -1 (mod n), siis on n tõenäoliselt algarv. Sellisel juhul minge testi tulemuse juurde. Kui võrdsus ebaõnnestub, korrake (${ displaystyle a ^ {4d}}$ ja nii edasi) kuni ${ displaystyle a ^ {2 ^ {s-1} d}}$.
   • Kui mingil etapil pärast ruudu muutmist muud kui ${ displaystyle pm 1}$ (mod n), saite +1 (mod n), seega n on liitarv. Kui ${ displaystyle a ^ {2 ^ {s-1} d} neq pm 1}$ (mod n), siis n ei ole prime.
   • Testi tulemus: kui n läbib testi, korrake seda teiste väärtuste puhul aenesekindluse suurendamiseks.

Osa 2/3: Kuidas lihtsustestid toimivad

1. 1 Jagajate loend. Definitsiooni järgi arv n on lihtne ainult siis, kui see ei ole jagatav 2 ja teiste täisarvudega, välja arvatud 1 ja ise. Ülaltoodud valem võimaldab teil eemaldada mittevajalikud sammud ja säästa aega: näiteks pärast seda, kui olete kontrollinud, kas arv jagub 3 -ga, pole vaja kontrollida, kas see jagub 9 -ga.
   • Funktsioon alam (x) ümardab x lähima täisarvuni, mis on väiksem või võrdne x -ga.
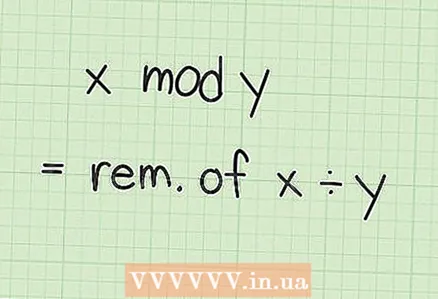2. 2 Lisateave modulaarse aritmeetika kohta. Operatsioon "x mod y" (mod on lühend ladinakeelsest sõnast "modulo", see tähendab "moodul") tähendab "jaga x y -ga ja leia ülejäänud". Teisisõnu, modulaarses aritmeetikas, teatud väärtuse saavutamisel, mida nimetatakse moodul, "pöörduvad" numbrid uuesti nulli. Näiteks loeb kell mooduliga 12 tagasi: see näitab 10, 11 ja 12 tundi ning naaseb seejärel 1 -le.
   • Paljudel kalkulaatoritel on mod -võti. Selle jaotise lõpus näidatakse, kuidas seda funktsiooni käsitsi arvutada suurte numbrite jaoks.
3. 3 Lugege Fermati väikese teoreemi lõkse. Kõik numbrid, mille jaoks katsetingimused ei ole täidetud, on liitühendid, kuid ülejäänud numbrid on ainult ilmselt on lihtsad. Kui soovite vältida valesid tulemusi, otsige n loendis "Carmichaeli numbrid" (liitanumbrid, mis vastavad sellele testile) ja "Fermati pseudoprime numbrid" (need numbrid vastavad katsetingimustele ainult mõne väärtuse puhul) a).
4. 4 Kui see on mugav, kasutage Miller-Rabini testi. Kuigi see meetod on käsitsi arvutamiseks üsna tülikas, kasutatakse seda sageli arvutiprogrammides. See tagab vastuvõetava kiiruse ja vähem vigu kui Fermati meetod. Liitnumbrit ei võeta algarvuna, kui arvutused tehakse rohkem kui ¼ väärtuste jaoks a... Kui valite juhuslikult erinevaid väärtusi a ja kõigi nende puhul annab test positiivse tulemuse, võime üsna kindlalt eeldada, et n on algarv.
5. 5 Suure arvu korral kasutage modulaarset aritmeetikat. Kui teil pole modifikatsioonikalkulaatorit käepärast või kui kalkulaator ei ole mõeldud nii suurte numbrite käsitlemiseks, kasutage arvutuste hõlbustamiseks võimsusomadusi ja modulaarset aritmeetikat. Allpool on näide ${ displaystyle 3 ^ {50}}$ mod 50:
   • Kirjutage avaldis mugavamas vormis ümber: ${ displaystyle (3 ^ {25} * 3 ^ {25})}$ mod 50. Manuaalsed arvutused võivad vajada täiendavaid lihtsustusi.
   • ${ displaystyle (3 ^ {25} * 3 ^ {25})}$ mod 50 = ${ displaystyle (3 ^ {25}})$ mod 50 ${ displaystyle * 3 ^ {25}}$ mod 50) mod 50. Siin võtsime arvesse moodulkorrutuse omadust.
   • ${ displaystyle 3 ^ {25}}$ mod 50 = 43.
   • ${ displaystyle (3 ^ {25}})$ mod 50 ${ displaystyle * 3 ^ {25}}$ mod 50) mod 50 = ${ displaystyle (43 * 43)}$ mod 50.
   • ${ displaystyle = 1849}$ mod 50.
   • ${ displaystyle = 49}$.

Osa 3 /3: Hiina järelejäänud teoreemi kasutamine

1. 1 Valige kaks numbrit. Üks numbritest peab olema kombineeritud ja teine ​​täpselt selline, mida soovite lihtsuse huvides testida.
   • Arv1 = 35
   • Arv 2 = 97
2. 2 Valige kaks väärtust, mis on suuremad kui null ja vastavalt väiksemad kui numbrid Number1 ja Number2. Need väärtused ei tohi olla samad.
   • Väärtus1 = 1
   • Väärtus2 = 2
3. 3 Arvutage numbrite 1 ja numbrite MMI (matemaatiline multiplikatiivne pöördvõrdeline).
   • Arvutage MMI
     • MMI1 = arv2 ^ -1 mod number1
     • MMI2 = arv1 ^ -1 mod number2
   • Ainult algarvude jaoks (see annab arvu liitarvude jaoks, kuid see ei ole tema MMI):
     • MMI1 = (arv2 ^ (arv1-2))% arv1
     • MMI2 = (arv1 ^ (arv2-2))% arv2
   • Näiteks:
     • MMI1 = (97 ^ 33)% 35
     • MMI2 = (35 ^ 95)% 97
4. 4 Looge iga MMI jaoks tabel kuni log2 mooduliteni:
   • MMI1 jaoks
     • F (1) = arv2% arv1 = 97% 35 = 27
     • F (2) = F (1) * F (1)% arv1 = 27 * 27% 35 = 29
     • F (4) = F (2) * F (2)% arv1 = 29 * 29% 35 = 1
     • F (8) = F (4) * F (4)% arv1 = 1 * 1% 35 = 1
     • F (16) = F (8) * F (8)% arv1 = 1 * 1% 35 = 1
     • F (32) = F (16) * F (16)% arv1 = 1 * 1% 35 = 1
   • Paaritud numbrite arvutamine 1 - 2
     • 35 -2 = 33 (10001) alus 2
     • MMI1 = F (33) = F (32) * F (1) mod 35
     • MMI1 = F (33) = 1 * 27 mod 35
     • MMI1 = 27
   • MMI2 jaoks
     • F (1) = arv1% arv2 = 35% 97 = 35
     • F (2) = F (1) * F (1)% arv2 = 35 * 35 mod 97 = 61
     • F (4) = F (2) * F (2)% arv2 = 61 * 61 mod 97 = 35
     • F (8) = F (4) * F (4)% Arv2 = 35 * 35 mod 97 = 61
     • F (16) = F (8) * F (8)% Arv2 = 61 * 61 mod 97 = 35
     • F (32) = F (16) * F (16)% Arv2 = 35 * 35 mod 97 = 61
     • F (64) = F (32) * F (32)% Arv2 = 61 * 61 mod 97 = 35
     • F (128) = F (64) * F (64)% Arv2 = 35 * 35 mod 97 = 61
   • Arvutage paarisarv 2 - 2
     • 97 - 2 = 95 = (1011111) alus 2
     • MMI2 = ((((((F (64) * F (16)% 97) * F (8)% 97) * F (4)% 97) * F (2)% 97) * F (1)% 97)
     • MMI2 = ((((((35 * 35)% 97) * 61)% 97) * 35% 97) * 61% 97) * 35% 97)
     • MMI2 = 61
5. 5 Arvuta (väärtus1 * arv2 * MMI1 + väärtus2 * arv1 * MMI2)% (arv1 * arv2)
   • Vastus = (1 * 97 * 27 + 2 * 35 * 61)% (97 * 35)
   • Vastus = (2619 + 4270)% 3395
   • Vastus = 99
6. 6 Veenduge, et number1 pole esmatähtis
   • Arvuta (vastus - väärtus1)% arv1
   • 99 – 1 % 35 = 28
   • Kuna 28 on suurem kui 0, pole 35 algarv.
7. 7 Kontrollige, kas number 2 on peamine.
   • Arvuta (vastus - väärtus2)% arv2
   • 99 – 2 % 97 = 0
   • Kuna 0 on 0, on 97 tõenäoliselt algarv.
8. 8 Korrake samme 1 kuni 7 veel vähemalt kaks korda.
   • Kui saate punktis 7 0:
     • Kasutage teistsugust numbrit1, kui number1 pole esmane.
     • Kasutage teist numbrit1, kui number1 on peamine. Sel juhul peaksite 6. ja 7. sammuga saama 0.
     • Kasutage erinevat tähendust1 ja tähendust2.
   • Kui sammus 7 saate järjekindlalt 0, siis on number 2 suure tõenäosusega esmane.
   • Sammud 1 kuni 7 võivad põhjustada vea, kui Number1 ei ole primaarne ja Number2 on arvu 1 jagaja. Kirjeldatud meetod töötab kõigil juhtudel, kui mõlemad numbrid on algarvud.
   • Peate samme 1 kuni 7 kordama seetõttu, et mõnel juhul, isegi kui number1 ja number 2 pole esmased, saate sammus 7 0 (ühe või mõlema numbri jaoks). Seda juhtub harva.Valige mõni muu arv1 (liit) ja kui arv2 ei ole esmane, siis number 2 ei võrdu sammuga 7 nulliga (välja arvatud juhul, kui arv1 on arvu 2 jagaja - siin on primes alati sammus 7 null).

Näpunäiteid

• Algarvud vahemikus 168 kuni 1000: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79 , 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211 , 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359 , 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509 , 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673 , 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853 , 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997.
• Kuigi toore jõu testimine on suurte numbritega töötamisel tüütu test, on see väikeste numbrite puhul üsna tõhus. Isegi suurte numbrite puhul alustage väikeste jagajate testimisest ja seejärel liikuge keerukamate meetodite juurde numbrite lihtsuse kontrollimiseks (kui väikesi jagajaid ei leita).

Mida sul vaja on

• Paber, pliiats või arvuti