Sisu

• Astuda
• 1. osa 4-st: maatriksi koostamine
• 4. osa 2: Maatriksiga süsteemi lahendamise toimingute õppimine
• 3. osa 4-st: ühendage sammud galaktika lahendamiseks
• 4. osa 4-st: lahenduse kontrollimine
• Näpunäited

Maatriks on väga kasulik viis numbrite esitamiseks plokivormingus, mida saate seejärel kasutada lineaarvõrrandisüsteemi lahendamiseks. Kui teil on ainult kaks muutujat, kasutate tõenäoliselt erinevat meetodit. Nende muude meetodite näidete kohta lugege sellest jaotisest Võrrandisüsteemi lahendamine. Kuid kui teil on kolm või enam muutujat, on massiiv ideaalne. Kasutades korrutamise ja liitmise korduvaid kombinatsioone, saate süsteemse lahenduseni jõuda.

Astuda

1. osa 4-st: maatriksi koostamine

1. Veenduge, et teil oleks piisavalt andmeid. Maatriksi abil lineaarses süsteemis iga muutuja jaoks ainulaadse lahenduse saamiseks peab teil olema nii palju võrrandeid kui arv muutujaid, mida proovite lahendada. Näiteks: muutujatega x, y ja z vajate kolme võrrandit. Kui teil on neli muutujat, vajate nelja võrrandit.
   • Kui teil on muutujate arvust vähem võrrandeid, saate teada muutujate mõned piirid (näiteks x = 3y ja y = 2z), kuid täpset lahendust ei saa. Selle artikli jaoks töötame ainult ainulaadse lahenduse nimel.
2. Kirjutage oma võrrandid standardkujule. Enne kui võrranditest andmeid maatrikskujule panna, kirjutage iga võrrand kõigepealt standardkujule. Lineaarvõrrandi standardvorm on Ax + By + Cz = D, kus suurtähed on koefitsiendid (numbrid) ja viimane number (D selles näites) on võrdusmärgist paremal.
   • Kui teil on rohkem muutujaid, jätkake lihtsalt rida nii kaua kui vaja. Näiteks kui proovisite kuue muutujaga süsteemi lahendada, näeks teie vaikekuju välja nagu Au + Bv + Cw + Dx + Ey + Fz = G. Selles artiklis keskendume süsteemidele, millel on ainult kolm muutujat. Suurema galaktika lahendamine on täpselt sama, kuid võtab lihtsalt rohkem aega ja rohkem samme.
   • Pange tähele, et standardses vormis on terminite vahelised toimingud alati täienduseks. Kui teie võrrandis on lahutamine, siis liitmise asemel peate sellega hiljem töötama, muutes oma koefitsiendi negatiivseks. Selle meeldejätmise hõlbustamiseks võite võrrandi ümber kirjutada ja operatsiooni lisada ning koefitsiendi muuta negatiivseks. Näiteks võite võrrandi 3x-2y + 4z = 1 ümber kirjutada kui 3x + (- 2y) + 4z = 1.
3. Pange võrrandisüsteemi numbrid maatriksisse. Maatriks on arvude rühm, mis on paigutatud omamoodi tabelisse, mille abil me töötame süsteemi lahendamiseks. Põhimõtteliselt sisaldab see samu andmeid kui võrrandid ise, kuid lihtsamas vormingus. Oma võrrandite maatriksi valmistamiseks standardsel kujul kopeerige iga võrrandi koefitsiendid ja tulemus ühele reale ning virnastage need read üksteise peale.
   • Oletame, et teil on süsteem, mis koosneb kolmest võrrandist 3x + y-z = 9, 2x-2y + z = -3 ja x + y + z = 7. Teie maatriksi ülemine rida sisaldab numbreid 3, 1, -1, 9, kuna need on koefitsiendid ja esimese võrrandi lahendus. Pange tähele, et eeldatakse, et kõigi muutujate puhul, millel puudub koefitsient, on koefitsient 1. Maatriksi teisest reast saab 2, -2, 1, -3 ja kolmandast reast 1, 1, 1, 7.
   • Joondage kindlasti esimeses veerus x koefitsiendid, teises y koefitsiendid, kolmandas z koefitsiendid ja neljandas lahenditerminid. Kui olete maatriksiga töötanud, on need veerud lahenduse kirjutamisel olulised.
4. Joonista kogu maatriksi ümber suur nurksulg. Kokkuleppe kohaselt tähistatakse maatriksit nurksulgude paariga [] kogu arvude ploki ümber. Sulgudes ei ole lahendus kuidagi mõjutatud, kuid need näitavad, et töötate maatriksitega. Maatriks võib koosneda suvalisest arvust ridadest ja veergudest. Selles artiklis kasutame järjest sulgude ümber sulgusid, et osutada nende koosseisule.
5. Levinud sümboolika kasutamine. Maatriksitega töötamisel on tavaline viidata ridadele lühendiga R ja veergudele lühendiga C. Konkreetse rea või veeru tähistamiseks võite kasutada nende tähtedega numbreid. Näiteks maatriksi 1. rea tähistamiseks võite kirjutada R1. Seejärel saab 2. reast R2.
   • Maatriksis saate märkida mis tahes konkreetse positsiooni, kasutades R ja C kombinatsiooni. Näiteks teise rea, kolmanda veeru mõiste tähistamiseks võite seda nimetada R2C3.

4. osa 2: Maatriksiga süsteemi lahendamise toimingute õppimine

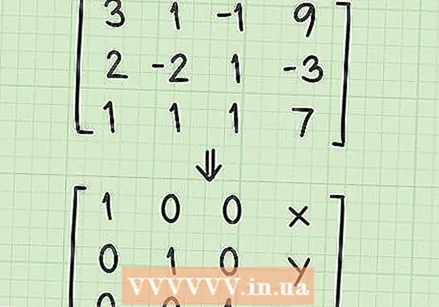1. Mõista lahuse maatriksi kuju. Enne võrrandisüsteemi lahendamise alustamist peate mõistma, mida maatriksiga teete. Sel hetkel on teil maatriks, mis näeb välja selline:
   • 3 1 -1 9
   • 2 -2 1 -3
   • 1 1 1 7
   • "Lahendusmaatriksi" loomiseks töötate paljude põhitoimingutega. Lahendusmaatriks näeb välja selline:
   • 1 0 0 x
   • 0 1 0 a
   • 0 0 1 z
   • Pange tähele, et maatriks koosneb 1-st diagonaaljoonel ja 0-ga kõigis muudes ruumides, välja arvatud neljas veerg. Neljanda veeru numbrid on muutujate x, y ja z lahendus.
2. Kasutage skalaarkorrutist. Esimene teie käsutuses olev vahend maatriksi abil süsteemi lahendamiseks on skalaarne korrutamine. See on lihtsalt termin, mis tähendab, et korrutate maatriksi rea elemendid konstantse arvuga (mitte muutujaga). Skalaarse korrutamise kasutamisel pidage meeles, et peate korrutama kogu rea iga termini valitud arvuga. Kui unustate esimese termini ja lihtsalt korrutate, saate vale lahenduse. Kuid te ei pea kogu maatriksit korraga korrutama. Skalaarkorrutuses töötate korraga ainult ühel real.
   • Murdude kasutamine skalaarkorrutuses on tavaline, kuna soovite sageli saada 1-ga diagonaalset rida. Harju töötama murdudega. Samuti on lihtsam (enamiku maatriksi lahendamise etappide jaoks) osata kirjutada oma murdosad vales vormis, seejärel teisendada need lõpliku lahenduse jaoks segasinumbriteks. Seetõttu on numbriga 1 2/3 lihtsam töötada, kui kirjutate selle 5/3.
   • Näiteks algab meie näiteülesande esimene rida (R1) mõistetega [3,1, -1,9]. Lahuse maatriksis peab esimese rea esimeses positsioonis olema tähis 1. 3 "muutmiseks" 1-ks saame korrutada kogu rea 1/3-ga. See loob uue R1 väärtuse [1,1 / 3, -1 / 3,3].
   • Jätke negatiivsed märgid kindlasti sinna, kuhu nad kuuluvad.
3. Kasutage rea liitmist või lahutamist. Teine tööriist, mida saate kasutada, on kahe maatriksi rea liitmine või lahutamine. 0-termini loomiseks oma lahenduste maatriksis peate 0-le jõudmiseks lisama või lahutama numbreid. Näiteks kui R1 on maatriks [1,4,3,2] ja R2 on [1,3,5,8], siis võite esimese rea teisest lahutada ja luua uue rea [0, -1, 2,6], sest 1-1 = 0 (esimene veerg), 3-4 = -1 (teine ​​veerg), 5-3 = 2 (kolmas veerg) ja 8-2 = 6 (neljas veerg). Rea lisamise või lahutamise korral kirjutage oma uus tulemus selle rea asemel, millega te alustasite. Sel juhul ekstraheerime rida 2 ja sisestame uue rea [0, -1,2,6].
   • Võite kasutada kiiret tähistust ja kuulutada selle toimingu väärtuseks R2-R1 = [0, -1,2,6].
   • Pidage meeles, et liitmine ja lahutamine on sama toimingu vastandvormid. Mõelge sellele kui kahe numbri liitmisele või vastupidi lahutamisele. Näiteks kui alustate lihtsa võrrandiga 3-3 = 0, võite mõelda sellele kui liitumisülesandele 3 + (- 3) = 0. Tulemus on sama. See tundub lihtne, kuid mõnikord on probleemi ühel või teisel kujul lihtsam kaaluda. Hoidke lihtsalt silma peal oma negatiivsetel märkidel.
4. Kombineerige ridade liitmine ja skalaarne korrutamine ühes etapis. Te ei saa eeldada, et tingimused vastavad alati, nii et saate oma maatriksisse 0-de loomiseks kasutada lihtsat liitmist või lahutamist. Sagedamini peate lisama (või lahutama) teisest reast mitu. Selleks peate kõigepealt korrutama skalaari, seejärel lisama selle tulemuse sihtreale, mida proovite muuta.
   • Oletame; et rida 1 on [1,1,2,6] ja rida 2 on [2,3,1,1]. Soovite R2 esimesse veergu 0-mõistet. See tähendab, et soovite muuta 2 väärtuseks 0. Selleks peate lahutama 2. 2 saate, korrutades esmalt rea 1 skalaarkorrutisega 2 ja lahutades seejärel esimese rea teisest reast. Lühidalt võib selle kirjutada kui R2-2 * R1. Kõigepealt korrutage R1 2-ga, et saada [2,2,4,12]. Seejärel lahutage see R2-st, et saada [(2-2), (3-2), (1-4), (1-12)]. Lihtsustage seda ja teie uus R2 on [0,1, -3, -11].
5. Kopeerige read, mis jäävad töötamise ajal muutumatuks. Maatriksil töötades muudate korraga ühte rida kas skalaarse korrutamise, rea liitmise või rea lahutamise või sammude kombinatsiooni abil. Ühe rea muutmisel kopeerige oma maatriksi ülejäänud read algsel kujul.
   • Levinud viga ilmneb kombineeritud korrutamis- ja liitmisetapi sooritamisel ühe liigutusega. Näiteks öelge, et peate kaks korda lahutama R1 R2-st. Kui korrutate selle sammu tegemiseks R1 2-ga, pidage meeles, et R1 ei muutu maatriksis. Korrutamine toimub ainult R2 muutmiseks. Esmalt kopeerige R1 algkujul ja seejärel muutke R2.
6. Esimene töö ülevalt alla. Süsteemi lahendamiseks töötate väga organiseeritud mustris, "lahendades" sisuliselt ühe maatriksi termini korraga. Kolme muutujaga massiivi järjestus näeb välja selline:
   • 1. Tehke esimese rea esimesse veergu 1 (R1C1).
   • 2. Tehke teise rea esimesse veergu 0 (R2C1).
   • 3. Tehke teises reas teises veerus 1 (R2C2).
   • 4. Tehke kolmanda rea ​​esimesse veergu 0 (R3C1).
   • 5. Tehke kolmandas reas teises veerus 0 (R3C2).
   • 6. Tehke kolmandas reas kolmandas veerus 1 (R3C3).
7. Koo tagasi alt üles. Kui teete sammud õigesti, olete lahenduse poole peal. Teil peab olema 1 diagonaaljoon, mille all on 0. Neljanda veeru numbritel pole praegu tähtsust. Nüüd töötate tagasi tippu järgmiselt:
   • Looge teises reas kolmandas veerus 0 (R2C3).
   • Looge 0 esimeses reas, kolmandas veerus (R1C3).
   • Looge esimese rea teises veerus 0 (R1C2).
8. Kontrollige, kas olete loonud lahenduste maatriksi. Kui teie töö on õige, olete loonud lahenduste maatriksi, mille esimese kolme veeru muudes positsioonides on R1C1, R2C2, R3C3 ja 0 diagonaaljoonel 1-d. Neljanda veeru numbrid on teie lineaarse süsteemi lahendused.

3. osa 4-st: ühendage sammud galaktika lahendamiseks

1. Alustage lineaarvõrrandite näidissüsteemist. Nende sammude harjutamiseks alustame varem kasutatud süsteemist: 3x + y-z = 9, 2x-2y + z = -3 ja x + y + z = 7. Kui kirjutate selle maatriksisse, on teil R1 = [3,1, -1,9], R2 = [2, -2,1, -3] ja R3 = [1,1,1,7].
2. Esimeses positsioonis R1C1 looge 1. Pange tähele, et R1 algab selles punktis numbriga 3. Peate selle muutma väärtuseks 1. Seda saate teha skalaarkorrutise abil, korrutades kõik R1 neli mõistet 1/3-ga. Lühidalt võite kirjutada R1 * 1/3. See annab R1 jaoks uue tulemuse, kui R1 = [1,1 / 3, -1 / 3,3]. Kopeerige R2 ja R2 muutmata kujul, kui R2 = [2, -2,1, -3] ja R3 = [1,1,1,7].
   • Pange tähele, et korrutamine ja jagamine on ainult üksteise pöördfunktsioonid. Võime öelda, et korrutame 1/3 või jagame 3-ga, tulemust muutmata.
3. Looge teises reas esimeses veerus 0 (R2C1). Siinkohal on R2 = [2, -2,1, -3]. Lahendusmaatriksile lähemale jõudmiseks peate muutma esimese termini 2-st 0-ni. Seda saab teha lahutades R1 väärtuse kaks korda, kuna R1 algab tähega 1. Lühidalt öeldes toiming R2- 2 * R1. Pidage meeles, et te ei muuda R1, vaid töötage sellega. Nii et esimene koopia R1, kui R1 = [1,1 / 3, -1 / 3,3]. Kui te kahekordistate R1 iga termini, saate 2 * R1 = [2,2 / 3, -2 / 3,6]. Lõpuks lahuta see tulemus algsest R2-st, et saada uus R2. Termini järgi töötades saab sellest lahutamisest (2-2), (-2-2 / 3), (1 - (- 2/3)), (-3-6). Lihtsustame neid uue R2-ga = [0, -8 / 3,5 / 3, -9]. Pange tähele, et esimene termin on 0 (mis iganes teie eesmärk oli).
   • Kirjutage rida 3 (mis pole muutunud) R3 = [1,1,1,7].
   • Negatiivsete arvude lahutamisel olge ettevaatlik, veendumaks, et märgid püsivad õiged.
   • Nüüd jätame kõigepealt murdosad nende sobimatul kujul. See muudab lahenduse hilisemad sammud lihtsamaks. Murde saab probleemi viimases etapis lihtsustada.
4. Looge teises reas teises veerus 1 (R2C2). 1-de diagonaaljoone moodustamise jätkamiseks peate teisendama teise termini -8/3 üheks. Tehke see, korrutades kogu rea selle numbri vastastikusega (-3/8). Sümboolselt on see samm R2 * (- 3/8). Saadud teine ​​rida on R2 = [0,1, -5 / 8,27 / 8].
   • Pange tähele, et kui rea vasak pool hakkab 0 ja 1 lahusega sarnanema, võib parem pool hakata kole välja nägema valede murdudega. Jäta nad lihtsalt selleks, mis nad praegu on.
   • Ärge unustage puutumata ridade kopeerimist jätkata, nii et R1 = [1,1 / 3, -1 / 3,3] ja R3 = [1,1,1,7].
5. Looge kolmandas reas esimeses veerus 0 (R3C1). Teie fookus liigub nüüd kolmandale reale, R3 = [1,1,1,7]. Esimesel positsioonil 0 tegemiseks peate lahutama 1 hetkel sellel positsioonil olevast 1-st. Kui vaatate üles, on R1 esimesel positsioonil 1. Nii et vajaliku tulemuse saamiseks peate R3-st lihtsalt lahutama R1. Termini tööperioodiks saab see (1-1), (1-1 / 3), (1 - (- 1/3)), (7-3). Seejärel saab neid nelja miniprobleemi lihtsustada uuele R3 = [0,2 / 3,4 / 3,4].
   • Jätkake kopeerimist mööda R1 = [1,1 / 3, -1 / 3,3] ja R2 = [0,1, -5 / 8,27 / 8]. Pidage meeles, et vahetate korraga ainult ühte rida.
6. Tehke kolmandas reas teises veerus 0 (R3C2). See väärtus on praegu 2/3, kuid see tuleb teisendada väärtuseks 0. Esmapilgul näib, et saate R1 väärtused kahekordistada, kuna R1 vastav veerg sisaldab 1/3. Kui aga kahekordistate ja lahutate kõik R1 väärtused, muutub R3 esimeses veerus 0, mida te ei soovi. See oleks teie lahenduses samm tagasi. Nii et peate töötama mõne R2 kombinatsiooniga. 2/3 lahutamine R2-st loob teises veerus 0, muutmata esimest veergu. Lühidalt on see R3-2 / 3 * R2. Üksikuteks mõisteteks saavad (0-0), (2 / 3-2 / 3), (4/3 - (- - 5/3 * 2/3)), (4-27 / 8 * 2/3) . Seejärel annab lihtsustamine R3 = [0,0,42 / 24,42 / 24].
7. Looge kolmandas reas kolmandas veerus 1 (R3C3). See on lihtne korrutamine selle arvu vastandiga, mida see ütleb. Praegune väärtus on 42/24, nii et saate soovitud väärtuse saamiseks korrutada 24/42-ga. Pange tähele, et kaks esimest mõistet on mõlemad 0, nii et kõik korrutised jäävad 0. Uus väärtus R3 = [0,0,1,1].
   • Pange tähele, et eelmises etapis üsna keerulisena tundunud murrud hakkavad juba lahenema.
   • Jätkake R1 = [1,1 / 3, -1 / 3,3] ja R2 = [0,1, -5 / 8,27 / 8].
   • Pange tähele, et sel hetkel on teie lahuse maatriksi diagonaal 1. Oma lahenduse leidmiseks peate teisendama ainult kolm maatriksi elementi 0-ks.
8. Looge teises reas kolmandas veerus 0. R2 on praegu [0,1, -5 / 8,27 / 8], kolmandas veerus on väärtus -5/8. Peate selle teisendama väärtuseks 0. See tähendab, et peate R3-ga tegema mõne toimingu, mis seisneb 5/8 lisamises. Kuna R3 vastav kolmas veerg on 1, peate korrutama kõik R3 väärtused 5/8-ga ja lisama tulemuse R2-le. Lühidalt öeldes on see R2 + 5/8 * R3. Termini tähtaeg on R2 = (0 + 0), (1 + 0), (-5 / 8 + 5/8), (27/8 + 5/8). Seda saab lihtsustada väärtusega R2 = [0,1,0,4].
   • Seejärel kopeerige R1 = [1,1 / 3, -1 / 3,3] ja R3 = [0,0,1,1].
9. Loo 0 esimeses reas, kolmandas veerus (R1C3). Esimene rida on praegu R1 = [1,1 / 3, -1 / 3,3]. Kolmanda veeru -1/3 peate teisendama väärtuseks 0, kasutades mõnda R3 kombinatsiooni. Te ei soovi R2-d kasutada, kuna R2 teises veerus olev 1 muudaks R1 valesti. Nii et korrutate R3 * 1/3 ja lisate tulemuse R1-le. Selle tähis on R1 + 1/3 * R3. Termini väljatöötamise mõiste annab tulemuseks R1 = (1 + 0), (1/3 + 0), (-1 / 3 + 1/3), (3 + 1/3). Saate seda lihtsustada uue väärtusega R1 = [1,1 / 3,0,10 / 3].
   • Kopeerige muutmata R2 = [0,1,0,4] ja R3 = [0,0,1,1].
10. Tehke esimeses reas teises veerus 0 (R1C2). Kui kõik on õigesti tehtud, peaks see olema viimane samm. Teise veeru 1/3 peate teisendama väärtuseks 0. Selle saate korrutades ja lahutades R2 * 1/3. Lühidalt, see on R1-1 / 3 * R2. Tulemuseks on R1 = (1-0), (1 / 3-1 / 3), (0-0), (10 / 3-4 / 3). Seejärel annab lihtsustamine R1 = [1,0,0,2].
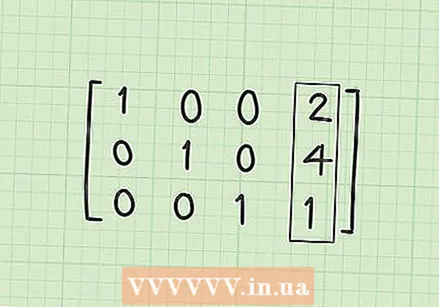11. Otsige lahuse maatriksit. Siinkohal, kui kõik sujuks, oleks teil kolm rida R1 = [1,0,0,2], R2 = [0,1,0,4] ja R3 = [0,0,1,1] peab olema. Pange tähele, et kui kirjutate selle plokkmaatriksivormi ridade üksteise kohal, on teil diagonaal 1-d 0-ga ja teie lahendused asuvad neljandas veerus. Lahendusmaatriks peaks välja nägema selline:
    • 1 0 0 2
    • 0 1 0 4
    • 0 0 1 1
12. Teie lahenduse mõistmine. Pärast lineaarvõrrandite teisendamist maatriksiks panete x koefitsiendid esimesse veergu, y koefitsiendid teise veergu, z koefitsiendid kolmandasse veergu. Kui soovite maatriksi uuesti võrranditeks ümber kirjutada, tähendavad need maatriksi kolm rida tegelikult kolme võrrandit 1x + 0y + 0z = 2, 0x + 1y + 0z = 4 ja 0x + 0y + 1z = 1. Kuna me võime 0 termini maha tõmmata ja 1 koefitsienti kirjutama ei pea, lihtsustavad need kolm võrrandit lahendusena, x = 2, y = 4 ja z = 1. See on lahendus teie lineaarvõrrandite süsteemile.

4. osa 4-st: lahenduse kontrollimine

1. Lisage lahused iga võrrandi igasse muutujasse. Alati on hea kontrollida, kas teie lahendus on tegelikult õige. Teete seda, testides tulemusi algvõrrandites.
   • Selle probleemi algsed võrrandid olid: 3x + y-z = 9, 2x-2y + z = -3 ja x + y + z = 7. Kui asendate muutujad leitud väärtustega, saate 3 * 2 + 4-1 = 9, 2 * 2-2 * 4 + 1 = -3 ja 2 + 4 + 1 = 7.
2. Lihtsustage mis tahes võrdlust. Tehke igas võrrandis toimingud vastavalt toimingute põhireeglitele. Esimene võrrand lihtsustub väärtusele 6 + 4-1 = 9 või 9 = 9. Teise võrrandi saab lihtsustada väärtuseks 4-8 + 1 = -3 või -3 = -3. Viimane võrrand on lihtsalt 7 = 7.
   • Kuna mis tahes võrrand lihtsustub tõelise matemaatilise lause saamiseks, on teie lahendid õiged. Kui mõni lahendus on vale, kontrollige oma tööd uuesti ja otsige vigu. Mõned levinumad vead ilmnevad siis, kui teel vabanevad miinusmärkidest või ajavad segi murdude korrutamise ja liitmise.
3. Kirjutage välja oma lõplikud lahendused. Selle antud ülesande korral on lõplik lahendus x = 2, y = 4 ja z = 1.

Näpunäited

• Kui teie võrrandisüsteem on väga keeruline ja paljude muutujatega, võite töö käsitsi tegemise asemel kasutada graafikakalkulaatorit. Selle kohta saate teavet ka wikiHow kohta.