Kuidas maatriksit jagada

Videot: MAATRIKS - Loodus ja kvantmaailm

Sisu

Lühike kokkuvõte
Sammud
Osa 1: 3: maatriksite jaguvuse testimine
Osa 2 /3: Pöördmaatriksi leidmine
Osa 3 /3: maatriksi korrutamine
Näpunäiteid
Hoiatused
Täiendavad artiklid

Kui teate kahte maatriksit korrutada, võite alustada maatriksite jagamist. Sõna „jagunemine” on jutumärkides, sest maatriksit ei saa tegelikult jagada. Jaotusoperatsioon asendatakse ühe maatriksi korrutamisega maatriksiga, mis on teise maatriksi pöördvõrdeline. Lihtsuse huvides kaaluge näidet täisarvudega: 10 ÷ 5. Leidke vastastikune väärtus 5: 5 või /₅, ja seejärel asendage jagamine korrutamisega: 10 x 5; jagamise ja korrutamise tulemus on sama. Seetõttu arvatakse, et jagamise saab asendada pöördmaatriksiga korrutamisega. Tavaliselt kasutatakse selliseid arvutusi lineaarvõrrandisüsteemide lahendamiseks.

Lühike kokkuvõte

Te ei saa maatriksit jagada. Jagamise asemel korrutatakse üks maatriks teise maatriksi pöördvõrdega. Kahe maatriksi [A] ÷ [B] "jaotus" kirjutatakse järgmiselt: [A] * [B] või [B] * [A].
Kui maatriks [B] ei ole ruut või kui selle determinant on 0, kirjutage üles "pole üheselt mõistetavat lahendust". Vastasel juhul leidke maatriksi [B] determinant ja jätkake järgmise sammuga.
Leidke vastupidine: [B].
Korrutage maatriksid, et leida [A] * [B] või [B] * [A]. Pidage meeles, et maatriksite korrutamise järjekord mõjutab lõpptulemust (see tähendab, et tulemused võivad erineda).

Sammud

Osa 1: 3: maatriksite jaguvuse testimine

1 Mõista maatriksite "jagunemist". Tegelikult ei saa maatriksit jagada. Sellist matemaatilist operatsiooni nagu “ühe maatriksi jagamine teisega” pole olemas. Jagamine asendatakse ühe maatriksi korrutamisega teise maatriksi pöördvõrdega. See tähendab, et märge [A] ÷ [B] ei ole õige, seega asendatakse see järgmise märkega: [A] * [B]. Kuna mõlemad kirjed on skalaarväärtuste puhul samaväärsed, võib teoreetiliselt rääkida maatriksite "jagamisest", kuid siiski on parem kasutada õiget terminoloogiat.
- Pange tähele, et [A] * [B] ja [B] * [A] on erinevad toimingud. Võimalike lahenduste leidmiseks võib osutuda vajalikuks teha mõlemad toimingud.
- Näiteks selle asemel ${ displaystyle { begin {pmatrix} 13 & 26 39 & 13 end {pmatrix}} div { begin {pmatrix} 7 & 4 2 & 3 end {pmatrix}}}$ Kirjuta üles ${ displaystyle { begin {pmatrix} 13 & 26 39 & 13 end {pmatrix}} * { begin {pmatrix} 7 & 4 2 & 3 end {pmatrix}} ^ {- 1} }$ .
  Võimalik, et peate arvutama ${ displaystyle { begin {pmatrix} 7 & 4 2 & 3 end {pmatrix}} ^ {- 1} * { begin {pmatrix} 13 ja 26 39 & 13 end {pmatrix}} }$ teistsuguse tulemuse saamiseks.
2 Veenduge, et maatriks, millega te teist maatriksit jagate, on ruudukujuline. Maatriksi ümberpööramiseks (maatriksi pöördvõrdelise leidmiseks) peab see olema ruut, st sama arvu ridade ja veergudega. Kui ümberpööratud maatriks ei ole pöördvõrdeline, pole kindlat lahendust.
- Jällegi pole maatriksid siin "jagatavad". Operatsioonis [A] * [B] viitab kirjeldatud tingimus maatriksile [B]. Meie näites viitab see tingimus maatriksile ${ displaystyle { begin {pmatrix} 7 ja 4 2 & 3 end {pmatrix}}}$
- Maatriksit, mida saab ümber pöörata, nimetatakse mitte-degenereerunud või korrapäraseks. Maatriksit, mida ei saa ümber pöörata, nimetatakse degeneratiivseks või ainsuseks.
3 Kontrollige, kas neid kahte maatriksit saab korrutada. Kahe maatriksi korrutamiseks peab esimese maatriksi veergude arv olema võrdne teise maatriksi ridade arvuga. Kui see tingimus pole täidetud kirjes [A] * [B] või [B] * [A], pole lahendust.
- Näiteks kui maatriksi [A] suurus on 4 x 3 ja maatriksi [B] suurus 2 x 2, pole lahendust. Te ei saa korrutada [A] * [B], sest 4 ≠ 2, ja te ei saa korrutada [B] * [A], sest 2 ≠ 3.
- Pange tähele, et pöördmaatriksil [B] on alati sama palju ridu ja veerge kui algsel maatriksil [B]. Kahe maatriksi korrutamise kontrollimiseks ei ole vaja pöördmaatriksit leida.
- Meie näites on mõlema maatriksi suurus 2 x 2, nii et neid saab korrutada mis tahes järjekorras.
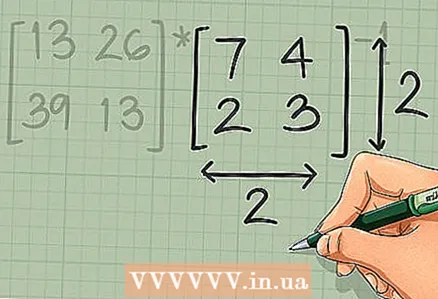
4 Leidke maatriksi 2 × 2 determinant. Pidage meeles: maatriksit saab ümber pöörata ainult siis, kui selle determinant ei ole null (vastasel juhul ei saa maatriksit ümber pöörata). 2 x 2 maatriksi determinandi leidmiseks tehke järgmist.
- 2 x 2 maatriks: maatriksi determinant ${ displaystyle { begin {pmatrix} a & b c & d end {pmatrix}}}$ on võrdne ad - bc. See tähendab, et põhidiagonaali elementide korrutisest (läbib vasakut ülemist ja paremat alumist nurka) lahutage teise diagonaali elementide korrutised (läbib paremat ülemist ja vasakut alumist nurka).
- Näiteks maatriksi determinant ${ displaystyle { begin {pmatrix} 7 ja 4 2 & 3 end {pmatrix}}}$ on võrdne (7) (3) - (4) (2) = 21 - 8 = 13. Determinant on nullivaba, seega saab selle maatriksi ümber pöörata.
5 Leidke suurema maatriksi determinant. Kui maatriksi suurus on 3 x 3 või rohkem, on determinanti veidi raskem arvutada.
- 3 x 3 maatriks: valige ükskõik milline üksus ja kriipsutage läbi rida ja veerg, milles see on.Leidke saadud 2 × 2 maatriksi determinant ja korrutage see valitud elemendiga; määrake determinandi märk spetsiaalses tabelis. Korrake seda protsessi ülejäänud kahe üksusega, mis on teie valitud elemendiga samas reas või veerus. Seejärel leidke saadud (kolme) määraja summa. Sellest artiklist leiate lisateavet 3 x 3 maatriksi determinandi leidmise kohta.
- Suured maatriksid: selliste maatriksite määrajat on kõige parem otsida graafilise kalkulaatori või tarkvara abil. Meetod sarnaneb 3 × 3 maatriksi determinandi leidmise meetodiga, kuid käsitsi rakendamine on üsna tüütu. Näiteks 4 x 4 maatriksi determinandi leidmiseks peate leidma nelja 3 x 3 maatriksi determinandid.
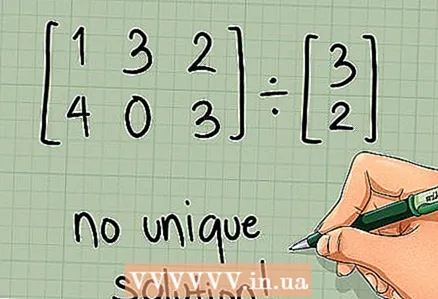6 Jätkake arvutusi. Kui maatriks pole ruudukujuline või kui selle determinant on võrdne nulliga, kirjutage "pole üheselt mõistetavat lahendit", see tähendab, et arvutusprotsess on lõpule viidud. Kui maatriks on ruudukujuline ja sellel on nullist erinev determinant, jätkake järgmise jaotisega.

Osa 2 /3: Pöördmaatriksi leidmine

1 Vahetage maatriksi 2 x 2 põhidiagonaali elemendid. Arvestades maatriksit 2 × 2, kasutage kiiret pöördmeetodit. Esiteks vahetage ülemine vasakpoolne element ja alumine parempoolne element. Näiteks:
- ${ displaystyle { begin {pmatrix} 7 ja 4 2 & 3 end {pmatrix}}}$ → ${ displaystyle { begin {pmatrix} 3 ja 4 2 & 7 end {pmatrix}}}$
- Märge: enamik inimesi kasutab 3 x 3 (või suurema) maatriksi ümberpööramiseks kalkulaatoreid. Kui peate seda käsitsi tegema, minge selle jaotise lõppu.
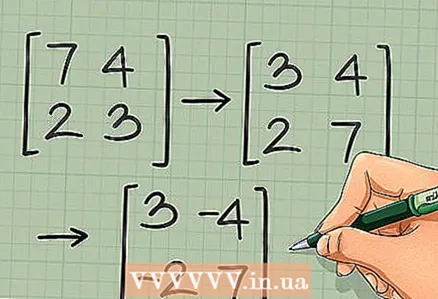2 Ärge vahetage ülejäänud kahte elementi, vaid muutke nende märki. See tähendab, et korrutage ülemine parempoolne element ja alumine vasakpoolne element -1-ga:
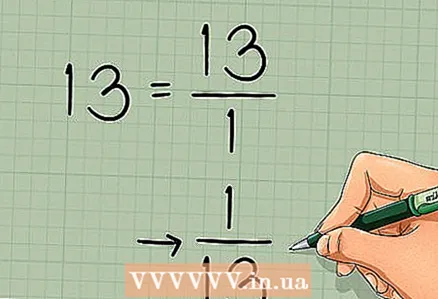- ${ displaystyle { begin {pmatrix} 3 ja 4 2 & 7 end {pmatrix}}}$ → ${ displaystyle { begin {pmatrix} 3 & -4 - 2 & 7 end {pmatrix}}}$
3 Leidke determinandi vastastik. Selle maatriksi determinant leiti eelmisest lõigust, nii et me ei hakka seda uuesti arvutama. Determinandi pöördväärtus kirjutatakse järgmiselt: 1 / (determinant):
- Meie näites on determinant 13. Pöördväärtus: ${ displaystyle { frac {1} {13}}}$ .
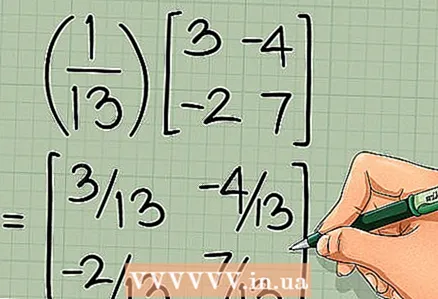4 Korrutage saadud maatriks determinandi pöördväärtusega. Korrutage iga uue maatriksi element determinandi pöördväärtusega. Lõplik maatriks on algse 2 x 2 maatriksi pöördvõrdeline:
- ${ displaystyle { frac {1} {13}} * { begin {pmatrix} 3 & -4 - 2 & 7 end {pmatrix}}}$
  = ${ displaystyle { begin {pmatrix} { frac {3} {13}} & { frac {-4} {13}} { frac {-2} {13}} ja { frac {7 } {13}} lõpp {pmatrix}}}$
5 Kontrollige, kas arvutused on õiged. Selleks korrutage algne maatriks selle pöördvõrdega. Kui arvutused on õiged, annab algse maatriksi korrutis pöördvõrdeliselt identsusmaatriksi: (1001){ displaystyle { begin {pmatrix} 1 & 0 0 & 1 end {pmatrix}}}... Kui test õnnestus, jätkake järgmise jaotisega.
- Meie näites: ${ displaystyle { begin {pmatrix} { frac {3} {13}} & { frac {-4} {13}} { frac {-2} {13}} ja { frac {7 } {13}} end {pmatrix}} * { begin {pmatrix} 7 & 4 2 & 3 end {pmatrix}} = { begin {pmatrix} 1 & 0 0 & 1 end {pmatrix}}}$ .
- Lisateavet maatriksite korrutamise kohta leiate sellest artiklist.
- Märkus: maatriksi korrutamise operatsioon ei ole kommutatiivne, st maatriksite järjestus on oluline. Kuid kui algne maatriks korrutatakse selle pöördvõrdega, viib mis tahes järjekord identiteedimaatriksini.
6 Leidke 3 x 3 maatriksi pöördvõrdeline osa (või suurem). Kui olete selle protsessiga juba tuttav, on parem kasutada graafilist kalkulaatorit või spetsiaalset tarkvara. Kui peate pöördmaatriksi käsitsi leidma, kirjeldatakse seda protsessi lühidalt allpool.
- Ühendage identiteedimaatriks I algse maatriksi paremal küljel. Näiteks [B] → [B | Mina]. Identiteedimaatriksi puhul on kõik põhidiagonaali elemendid võrdsed 1 ja kõik muud elemendid 0.
- Lihtsustage maatriksit nii, et selle vasak külg muutuks astmeliseks; jätkake lihtsustamist, nii et vasakust küljest saab identiteedimaatriks.
- Pärast lihtsustamist saab maatriksi järgmisel kujul: [I | B]. See tähendab, et selle parem külg on algse maatriksi pöördvõrdeline.

Osa 3 /3: maatriksi korrutamine

1 Kirjutage üles kaks võimalikku väljendit. Kahe skalaari korrutamise operatsioon on kommutatiivne, see tähendab 2 x 6 = 6 x 2.See ei kehti maatriksi korrutamise korral, seega peate võib -olla lahendama kaks avaldist:
- x = [A] * [B] on võrrandi lahendus x[B] = [A].
- x = [B] * [A] on lahendus võrrandile [B]x = [A].
- Tehke iga matemaatikatehing võrrandi mõlemal küljel. Kui [A] = [C], siis [B] [A] ≠ [C] [B], kuna [B] asub [A] -st vasakul, kuid [C] -st paremal.
2 Määrake lõpliku maatriksi suurus. Lõpliku maatriksi suurus sõltub korrutatud maatriksite suurusest. Lõpliku maatriksi ridade arv on võrdne esimese maatriksi ridade arvuga ja lõpliku maatriksi veergude arv võrdub teise maatriksi veergude arvuga.
- Meie näites mõlema maatriksi suurus ${ displaystyle { begin {pmatrix} 13 ja 26 39 & 13 end {pmatrix}}}$ ja ${ displaystyle { begin {pmatrix} { frac {3} {13}} & { frac {-4} {13}} { frac {-2} {13}} ja { frac {7 } {13}} lõpp {pmatrix}}}$ on 2 x 2, seega on algse maatriksi suurus 2 x 2.
- Vaatleme keerukamat näidet: kui maatriksi [A] suurus on 4 x 3 ja maatriksi [B] suurus on 3 x 3, siis on lõplik maatriks [A] * [B] 4 x 3.
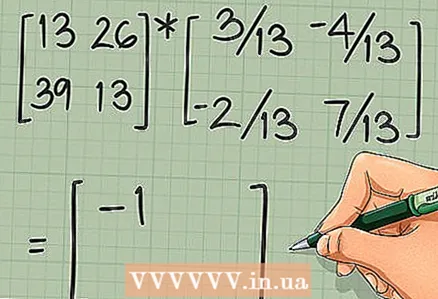3 Leidke esimese elemendi väärtus. Lugege seda artiklit või pidage meeles järgmisi põhilisi samme:
- Lõpliku maatriksi [A] [B] esimese elemendi (esimene rida, esimene veerg) leidmiseks arvutage maatriksi esimese rea [A] ja maatriksi [B] esimese veeru elementide punktide korrutis ]. 2 x 2 maatriksi puhul arvutatakse punkttoode järgmiselt: ${ displaystyle a_ {1,1} * b_ {1,1} + a_ {1,2} * b_ {2,1}}$ .
- Meie näites: ${ displaystyle { begin {pmatrix} 13 & 26 39 & 13 end {pmatrix}} * { begin {pmatrix} { frac {3} {13}} ja { frac {-4} { 13}} { frac {-2} {13}} ja { frac {7} {13}} end {pmatrix}}}$ ... Seega on lõpliku maatriksi esimene element järgmine element:
  ${ displaystyle (13 * { frac {3} {13}}) + (26 * { frac {-2} {13}})}$
  ${ displaystyle = 3 + -4}$
  ${ displaystyle = -1}$
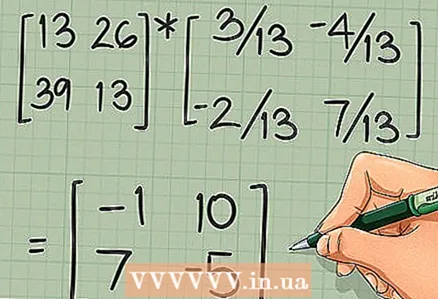4 Jätkake punkttoodete arvutamist, et leida lõpliku maatriksi iga element. Näiteks teises reas ja esimeses veerus paiknev element võrdub maatriksi [A] teise rea ja maatriksi [B] esimese veeru punktkorrutisega. Proovige ülejäänud esemed ise üles leida. Peaksite saama järgmised tulemused:
- ${ displaystyle { begin {pmatrix} 13 & 26 39 & 13 end {pmatrix}} * { begin {pmatrix} { frac {3} {13}} ja { frac {-4} { 13}} { frac {-2} {13}} ja { frac {7} {13}} end {pmatrix}} = { begin {pmatrix} -1 & 10 7 & -5 end {pmatrix}}}$
- Kui peate leidma mõne muu lahenduse: ${ displaystyle { begin {pmatrix} { frac {3} {13}} & { frac {-4} {13}} { frac {-2} {13}} ja { frac {7 } {13}} lõpp {pmatrix}} * { begin {pmatrix} 13 ja 26 39 & 13 end {pmatrix}} = { begin {pmatrix} -9 & 2 19 & 3 lõpp {pmatrix}}}$

Näpunäiteid

Maatriksi võib jagada skalaariks; selleks jagatakse maatriksi iga element skalaariga.
- Näiteks kui maatriks ${ displaystyle { begin {pmatrix} 6 & 8 2 & 4 end {pmatrix}}}$ jagades 2 -ga, saate maatriksi ${ displaystyle { begin {pmatrix} 3 ja 4 1 & 2 end {pmatrix}}}$

Hoiatused

Kalkulaator ei anna alati maatriksi arvutamisel absoluutselt täpseid tulemusi. Näiteks kui kalkulaator väidab, et üksus on väga väike arv (näiteks 2E), on väärtus tõenäoliselt null.